
 |
There is a consistent drop in the level of mathematical knowledge of students entering higher education. This is especially true on courses where mathematics is taught as a support subject. It therefore became necessary to devise a course to address the problem. The approach taken was to integrate different teaching and learning resources. Text based open teaming booklets, computer aided learning material and computer marked assessment are among these resources. The paper will discuss the different components of the course, how the course has developed, how it is implemented, the reactions of students to it, the results noted so far and intended future developments.
Since we are dealing with a such a wide variety of students with varied abilities and educational backgrounds an approach that can take into account their different styles and modes of learning was necessary. In order to do this a course was designed that combines several different teaching and learning resources. The subject matter that is included in the course is that of the basic mathematical tools that are required to teach the core syllabi on our degrees and is pre-calculus. The course that is now in use has evolved over several years, is still doing so and will continue to do so as new ideas and material emerge. The components all blend together to form an integrated learning resource.
It is important to use these resources to their best advantage in an integrated manner to form a complete learning package. Each individual resource is good on its own, but used together, in conjunction with other resources, each complementing the other, the resource that can be utilised is greatly increased and enhanced.
It was important to work with the students in the early stages to see where explanations were either not working or were not detailed enough, following which the necessary changes were made. Now the students are expected to work through the booklets on their own, bringing problems that arise to the tutor when help is required.
The booklets are also handy for the students to carry around in case an opportunity for study occurs.
A computer can be dynamic. Whereas a diagram or a graph on a written page is static. On a computer screen it can be animated or built up in stages. With a graph plotting package, for example, different parameters can be entered and experimentation can take place. Also investigations can be designed, all of which stimulate interest and bring about understanding.
Computers can also be interactive. When students are learning from a book, they are in complete charge of the learning process. In general the only action is on the student's part. With CAL the computer takes part in the action. The student might be asked to build up a diagram, to give the answer to a question, to change the input and watch the corresponding response or maybe to match up certain relevant items. In each of these cases there is an interaction between the student and the computer. It will give him/her feedback, giving praise when warranted, hints to help when needed and in the final instance the full and correct answer. The computer is playing the role of a tutor, giving help when required, controlling the student's progression till understanding has been gained and giving judgement when necessary.
CAL
So with the above attributes in mind, CAL packages were selected to go alongside the text booklets. As it takes a great deal of time to write this material, some CAL packages were purchased to use as a starting point. Some CAL has been written in house since, designed to enhance the subject matter from ie booklets, with diagrams, actions, examples built up stage by stage and chances for experimentation to take place. There will also be much more material becoming available soon when the UK. TLTP (Teaching and Learning Technology Programme) comes to fruition. This will be brought in to include in our resource.
Graph plotting package
This is an extremely valuable tool to use alongside the text. Tasks can he devised to allow experimentation to take place aimed at bringing about understanding of basic concepts. eg. gradients, intercepts, solutions of equations etc. Several of the booklets include sections which use this to enhance the understanding of a particular concept. Regular use of this encourages students to draw graphs to picture the problem they are working on and to gain greater insight into its possible solution.
Computer algebra package
There are many Computer Algebra packages available, but the one that was chosen was "Maple" for the reasons that it is both powerful and user friendly. This again allows experimentation. It will become increasingly more useful as the maths becomes more difficult, but it is still a useful tool at the foundation level. Also familiarity at this stage leads to a greater use further on. Again it is important to devise tasks and problems for the students to work on. A powerful tool such as this stimulates students to experiment for themselves and to ask questions regarding the output they generate.
Computer based assessment
Within a learning environment which is based upon student teacher interaction, the subjective assessment of student competence is not only straightforward, but in the majority of cases the most accurate assessment of student capabilities. In this setting formal assessment acts only as a selection tool.
As classes become larger and the student teacher relationship becomes more tenuous so the need for objective formal testing has increased. In an open learning environment regular objective tests have become an imperative, firstly to provide the student with the feedback they require to direct their own learning process, and secondly to prompt intervention by teachers when necessary.
At LMU the foundation mathematics course could be said to be delivered in a pseudo open learning structure, with traditional delivery methods being backed up by a variety of resources that encourage the student to assess and determine their own learning needs and capabilities.
Three strands of assessment have been and are still being developed, these are diagnostic testing, self assessment and formal assessment.
Diagnostic testing
It is understood that some students starting our courses have an adequate understanding of the subject matter in the Foundation Maths module, it is not the aim to make students 'clear hurdles' they have cleared before, all students are therefore asked to undertake a diagnostic exercise in their first week. The exercise breaks the course content into three blocks and determines whether a student is worthy of exemption from any of these three blocks. The result is that amongst the student body, individual students may be asked to study all, none or some of the course.
Self assessment Self assessment material has been available in text form probably for as long as text books, but if answers aren't provided to questions then they are likely to be of limited use in an open learning context, if answers are given at the back then the temptation to sneak a look can undermine effectiveness. The computer can overcome this by only providing answers after a question has been attempted unsuccessfully, the question structure that has been adopted allows two attempts at each question before providing the correct answer, in addition a repeat question is made available which re-presents the chosen question but with new data.
A secondary benefit is the ability of the computer to record student input for examination by a tutor, so that the student tutor interface is in fact not removed by use of the machine just separated by an intermediary. it is this separation which enables both student and tutor to be flexible in playing their 'part'.
The starting point was to provide a large bank of randomly delivered questions, for each of the 12 topics covered on the foundation maths course. This proved to have an unacceptable flaw in that there was no indication of the standard of question to be delivered and inevitably the weaker students would be delivered the most complex question first, which acted as a strong demotivator. However there was still a strong belief that questions delivered randomly from a large bank would provide a truly powerful resource that students would happily use as many times as they felt necessary.
The current solution (see Figure 1), which was arrived at via several piloted ideas, is to classify all questions into one of three categories dependent upon level of difficulty. The student starting at level one is given a number of questions from a large bank, with progress to higher levels linked to performance at that level; it is made clear to the student that this judgement is suggestive and it is simple to override the system and enter at any level. This structure combines the advantages of random selection whilst overcoming the earlier difficulty, it also has the added advantage of giving the student an extra insight into their progress, ie. have they reached level 1, 2 or 3.
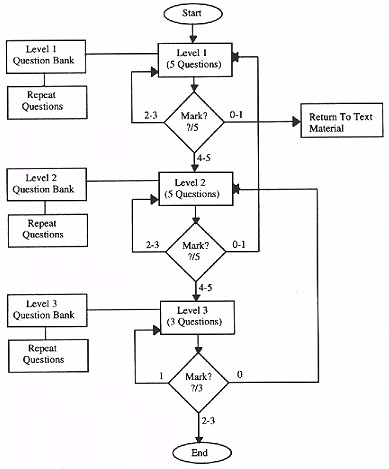
Figure 1
Formal assessment
The major role of formal assessment is very often for selection and grading purposes, in this context it is reasonable to suggest that assessing students on a simple right or wrong basis (as is the case with computer based packages) is inaccurate and unfair; in a mathematical context the working for an answer is as important as the answer itself.
In contrast formal mass examinations set against the clock have the drawback of forcing the pace of student learning and understanding up to and during the examination. Whereas computer marked tests offer the possibility of being flexible regarding the day the test is taken, and the time taken to complete the test.
At LMU we are learning to use both techniques as appropriate. On courses where foundation maths forms an essential mainstream part of the course the formal tests are used for continuous assessment, which is then coupled with more traditional paper tests to give as accurate a profile of student performance as possible. On other courses foundation maths is an adjunct to the main areas of study, performing the role of redressing inadequacies in student knowledge, such that all students have sufficient grounding in the subject regardless of educational background. In this setting the forma computer tests are used for monitoring rather than selection and as such have been deemed adequate for this purpose.
Each formal test encompasses four topics, with 12 topics in total this leads to 3 formal tests over the length of the module. Each test consists of up to ten questions, with each individual question being drawn from a random bank (see Figure 2). Students are able to take the tests during any surgery period, this has enabled the testing environment to be less clinical than mass paper based examinations, ie. the tests are open book and the student will take the tests when they feel ready.
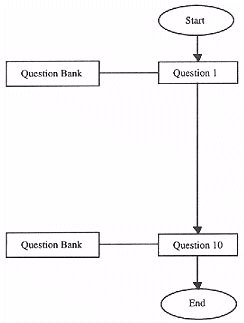
Figure 2
There is a "Mathematics Workshop" with fifteen Apple Macintosh computers. These are networked and deliver all the computer elements of the course. This workshop is run on an open access basis and is staffed each day during "surgery" times by an academic member of staff. Although LMU uses Apple Macs, the tests have also been written for use on PCs.
It is also important that the students accept the course as being accredited and compulsory for them to complete. Without this motivation they lose impetus, and tend to concentrate on the subjects that are accredited, seeing these as their first priority and this coming a poor second.
This year we have introduced the diagnostic testing for the first time. We hope that this will allow us to compare the level of the students' knowledge at the beginning of the course with that at the end.
With ever shrinking resources, the course has enabled us to cut down the staff contact time while at the same time presenting a course in an extremely professional and efficient manner and in a way that is attractive to students. It has also enabled us to monitor the performance of individual students and to give help or a push when it is required.
Moffat, J. M. (1994). An integrated approach for teaching mathematics using open learning. Paper delivered at Open Learning Foundation conference on Teaching Maths to non-Specialist Mathematicians, London, July 7-8.
| Authors: Jenifer Marshall and Paul Doney Faculty of Information and Engineering Systems Leeds Metropolitan University Calverley Street Leeds LS1 3HE Please cite as: Marshall, J. and Doney, P. (1996). OpenMath: An integrated course for the teaching and learning of foundation mathematics. In C. McBeath and R. Atkinson (Eds), Proceedings of the Third International Interactive Multimedia Symposium, 255-259. Perth, Western Australia, 21-25 January. Promaco Conventions. http://www.aset.org.au/confs/iims/1996/lp/marshall2.html |