
 |
Chaos has long been associated with disorder, a condition to be avoided. This paper will explore the more positive aspects of chaos which may prove beneficial to multimedia programmers. Having a basic understanding of the dynamics of non linear programming many comparisons can be drawn between multimedia and chaos. The paper illustrates how chaos can be of use to multimedia programmers. It establishes chaos's link with the dualities of order and disorder, initially by providing a short background study into features associated with chaos theory. The paper will suggest that chaos can act as a positive rather than negative factor in program design, assisting in the development of new modelling techniques. Looking specifically at elements such as the action of 'strange attractors', 'period doubling', 'non-linearity', the process of feedback and 'self similarity', thus providing the programmer with useful design 'templates'. Using templates offered by the above it is possible to plan and organise effective well conceived programs that have the potential to take the user to new levels of understanding using chaos theory as a basis.
The overuse of the term 'chaos' is one that has the chaologists (those who study chaos) of this world reeling. Hardly a day goes by without the word appearing in the news: chaos at sea, gun chaos, chaos in oil stocks, chaos at the school, and so on. We have all used the term usually to describe an uncontrollable event or system, yet in this paper I will try to dispel a few myths associated with the term chaos and actually show there are some positive sides to its somewhat tarnished character.
Before, however launching into the topic it would be useful to look at some of the characteristics of chaos, features found to be linked to chaotic behaviour. These include
The discovery of the strange attractor is yet another feature of chaos. Turbulence has long been a problem to many scientists. It is a mess, disorder on all scales, small deviations within larger ones. All standard rules tended to breakdown after a certain point, this was the onset of chaos. Fluids and gas could only behave in a steady predictable manner to a certain point, beyond this, random, non-predictable behaviour would occur. For many years this was considered to be how things were, scientists and engineers assumed that one could go no further. This phenomenon was never given a satisfactory explanation. The steady state often turns out to be not so steady. Dynamic systems are often influenced by seemingly minor factors. Also we have discovered that each element will act on other elements, this constant interaction can result in chaos.

Figure 1: A strange attractor
Bifurcation and period doubling have long been understood as factors that can have profound effects upon systems. A good example of how bifurcation works is to look at population behaviour. Some populations grow rapidly, others quickly die out, some rise and fall on a regular basis, others don't, these are acting under the laws governed by strange attractors and chaos.
It is seen as a type of non linear metamorphosis. The population example is very valuable in that it also points to the contribution of other factors. If a pair of rabbits were allowed to go on reproducing they would cover the entire universe in just 120 generations. This does not occur because of the other factors which influence populations, such as the availability of food, the action of disease, predators, etc. In fact the population size is dependent upon the whole environmental ecosystem. Period Doubling is now used to explain many of the previously unexplained problems associated with population biology and ecology (see Figure 2).
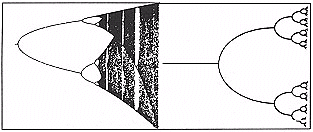
Figure 2: Branching at work
The common factor in the elements being described is that of non linearity. In the past we have been conditioned to think in a certain manner. This was mainly linear by design. Many systems were explained as natural progressions, one element following another. This for many was comfortable, it did not need to consider the possibility of external influences that may disrupt the systems direction. Linear equations are solvable, expressed on the straight line of a graph. Non linear systems are much more difficult to solve, as a result the type of mathematics necessary to fully understand them has been largely ignored. Today's science is now showing that nature is relentlessly non linear, we live in a non linear universe. The only straight lines are the ones we have created. It has been man's desire to make sense of the complex and seemingly random world by seeing it as a clockwork universe, all measurable and constrained. Science has now discovered that the clockwork universe simply does not work. Scientists are beginning to realise this and mathematicians are now working out concepts and techniques to face the reality of non linear dynamics.
An important feature of chaos theory is that of feedback or iteration. This is also a factor that is present within non linear systems. An example of feedback is that of audio feedback, the squeal of sonic feedback. If the microphone picks up a loud noise, this is amplified by the amplifier and speakers, which in turn is fed back into the microphone in an endless loop. It is this infinite feedback which Mandelbrot used to create the Mandelbrot Set, possibly the most complex mathematical form in the known universe. The Mandelbrot Set is a fractal, a visual expression of an iterative system. To create fractals such as the Mandelbrot Set the mathematics is usually ridiculously simple:
Z2 + C = Some number Mis the equation that drives this fractal. The sum of Z squared and C gives the result Z which becomes the equation's new starting point, this is repeated to infinity. C represents a series of complex numbers that the computer calculates. C's size is always finite no matter how many iterations the computer performs.

Figure 3: The Mandelbrot set
A fractal is a geometric figure that consists of an identical motif repeating itself on an ever reducing scale. A good example of this is the binary tree and the H-fractal. The H-fractal is a dendrite, named after the Greek dendron or tree. It is composed of ever smaller versions of the same H. It is in itself a self similar structure. Fractal structures such as the Mandelbrot are just one of the many forms to use the remarkable power of iterative function systems (IFS). This has lead to the development of a new form of geometry, fractal geometry. During the seventies the science of using mathematics to describe natural forms was in its infancy. The apparent relationship between them and chaos was completely unknown. They are now seen as mathematical relations. Fractals are a direct result of feedback and again are non linear in their formation. Scientists such as Benoit Mandelbrot, Michael Barnsley and Heige von Koch have all been experimenting with formulae that simulate natural forms. Fractal rivers in fractal landscapes complete with fractal clouds and skies are now possible. We have even been able to discover the rules which define the make up such complex forms as snowflakes, fern leaves, trees, weather patterns and more.
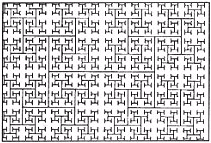
Figure 4: The "H" Fractal
Self similarity is yet another feature of chaos. We see self similarity at work within fractals, such as the H fractal mentioned above. Self similarity is as the name implies a repetition of form on an ever decreasing or increasing scale. The fractal of the Mandelbrot Set is a good example of self similarity at work. Zoom into this set and other smaller versions of the same are found, repeated onto infinity. This feature has captured the imagination of many scientists and artist alike. Other examples include tiny ice crystals, trees and mountain formations. The self similarity rule seems to appear everywhere. Not only do these structures appear in our environment as a whole but also within our own bodies. The human lungs again obey the fractal rules of self similarity and scale. The spiral, a very well known symbol, is also self similar in its structure, regardless how much you magnify it (see Figure 5).
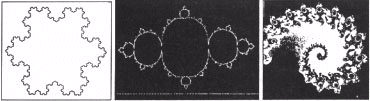
Figure 5:Fractal examples of self similarity
A factor that ties together all the above has been called universality. Mitchell Feigenbaum has done much to unlock its secrets. Universality offers the scientist the hope of solving hard problems merely by solving easy ones. This has made universality a hard pill for the scientific community to swallow. Feigenbaum's universality was not only qualitative, it was structural and metric. Using a pocket calculator, he tested a series of period doubling equations and found a universal scale to their transformations. They could then be applied to various phenomena such as electric circuitry, optical systems, solid state devices, business cycles, populations, and learning. He showed that the fine details in these systems don't really matter, period doubling is the common factor in the way order breaks down into chaos.
Universality is what others studying chaos where looking for, it offered them a model, a common means for describing their work. It was a model that everybody could understand. Today we find ourselves in a unique position, for the first time science can explain a phenomenon that governs all systems within an interconnected universe. The emerging science of 'wholeness', chaos theory.
One area this author has been researching is in the special relationships that exist between chaos and the creative design process. Its unique features of non-linearity and feedback to name just two are what multimedia programmers use constantly. By using chaos templates it is possible to help structure more meaningful and effective presentations.
One key feature of chaos is interactivity, chaos would simply not exist without it. Interactivity is not only important to chaos but to the multimedia ethos. So with this in mind let us now turn our attention to how we apply chaos and interactivity. An examination of the special chaotic elements mentioned will provide new insights into planning multimedia programs.
The action of strange attractors within dynamic systems can be quite profound. Strange Attractors cannot be controlled at any time. Taking the model illustrated (Fig 6.) will help programmers construct programs that either have a high or low degree of uncertainty by deliberately using or avoiding strange attractors.
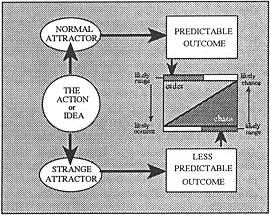
Figure 6: The action of strange attractors
Strange attractors manifest themselves in many ways, often the action goes completely undetected. The designer must first know where to look in order to have greater say in to what the likely design outcomes are likely to be. Within the area of multimedia planning the designer must be aware of the existence of normal attractors as opposed to strange attractors as these will impact upon the program's educational efficiency. That is to say, if a program does not allow for the manifestation of strange attractors (chaotic diversions) the positive elements of the multimedia presentation could be lost. Programmers should ensure that the design is robust enough to help overcome this. Error traps in future may need to take lessons from chaos. As programs become more complex and we move to multi-user systems the possibility of error is increased. Programmers in future may need to turn not only to having educators, graphic artists and sound programmers on their design teams, but also, sociologists, psychologists and chaologists.
Period doubling involves a single event branching through a process of change into two paths, each path then in turn breaking into two new paths, this goes on till the point of accumulation where predictable periodicity gives way to chaos. In order that multimedia programs can be adequately conceptualised it is sometimes necessary to generate new ideas from existing ones.
Chaos theory gives the program designer a framework in which to work. Using the fractal notion of branching enables the original idea to be quickly converted into new generations. Figure 7 illustrates how that in just five branches sixteen new ideas of concepts can be developed.
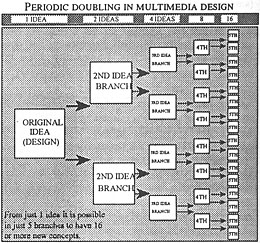
Figure 7: Branching at work
It is also possible to work in reverse order, zeroing in on one particular aspect or to give focus to a certain project.
In this case the designer has the task of choosing one idea from many. Using the branching structure indicated in Figure 7 enables the designer through selective filtering to arrive at the strongest and most applicable design. In multimedia design this provides the programmer with a template for not only developing ideas but also giving structure, ie, 'flow chart' creation.
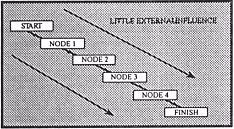
Figure 8: Linear design
In order to appreciate a non-linear approach we first must rethink what our philosophical base is to be. In modern programming the linear model simply doesn't work, it is too restrictive, too predictable in the production of outcomes. We now see the value of self referencing systems as found in non-linear models. Here responses from the participant are constantly being checked with the initial premise or starting point, results are then used to take the user to new levels, this serves to give the program greater directional efficiency. Nodes represent sections or program units, for example; background information data base, intermediate level information leading to advanced expert oriented data bases.
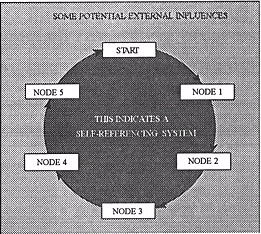
Figure 9: Non-linear design
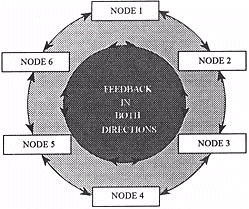
Figure 10: Feedback within design
The arrows on Figure 10 indicate feedback direction. In the linear model this feedback cannot exist since instruction is given and only flows in one direction (an authoritarian structure). Most involved in the learning process prefer a more democratic structure in which to work. Feedback is vital in all multimedia programming in that it allows participants greater access to new nodes of information with the ability to go forward or backwards to expand or consolidate the learning experience.
Within the design process if similar structures are employed throughout various stages of the multimedia program then the structure of the system as a whole is strengthened. Figure 11 shows how such a feature is easily incorporated within most design frameworks.
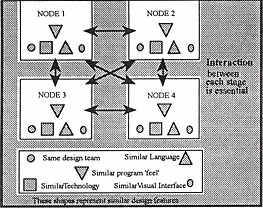
Figure 11: Self similarity at work
Hayles, N. Katherine (Ed) (1991). Chaos and order: Complex dynamics in literature and science. Chicago: University of Chicago Prem.
Briggs, J. and Peat, D. (1989). Turbulent mirror. New York: Harper and Row.
Stewart, Ian, (1990). Does God play dice. London: Penguin Books.
Gleick, James (1987). Chaos making: A new science. London: Sphere Books.
Lauwerier, Hans (1987). Fractals: Images of chaos. London: Penguin Books.
Olson, David (1993). Exploiting chaos: Cashing in on the realities of software development. New York: VNR Computing Library.
| Author: Greg Padfield, School of Design, Curtin University of Technology, GPO Box U1987, Perth WA 6001. Tel: 09 335 5154
Please cite as: Padfield, G. (1994). Chaos theory modelling in multimedia planning. In C. McBeath and R. Atkinson (Eds), Proceedings of the Second International Interactive Multimedia Symposium, 383-388. Perth, Western Australia, 23-28 January. Promaco Conventions. http://www.aset.org.au/confs/iims/1994/np/padfield.html |